| art theory 101~GoDNA: The Geometry of DNA (axial view) |
|---|
GoDNA: THE GEOMETRY OF DNA
© 2001, Reginald Brooks. All rights reserved.
- INTRODUCTION
- GEOMETRIC PATTERNS IN DNA
- NUMBER PATTERNS IN DNA
- (8.) STRUCTURE & CHEMISTRY OF DNA
- CONCLUSION
One of the most fundamental levels of Nature that we can both abstract and actualize is numbers...simple, quantifying numbers. Apparently Nature, here too, or should we say, fundamentally here, has chosen to create patterns of order, symmetry and aesthetic appeal in the ability to form diversity, richness and harmonious, resonating interconnections of the parts to the whole in everything from the simplest sequence of whole integer numbers to the supremely beautiful and highly sophisticated DNA double helix. Perhaps it is only inevitable that within the geometry, the numbers which describe the double helix...that rarest of molecular architecture demonstrating both self-replication and vector fabrication...should themselves be a repository of numerical magic.
The series of concentric double pentagons which inform the composite axial view of the DNA double helix are shown to contain a vast self-replication and growth potential built into the molecule itself. Mathematicians, artists, designers and engineers have known for centuries astonishing, almost magical, patterns in prime and geometric series, magic squares, and the special sequences and proportions such as Pascal's Triangle, the Golden Mean, the Fibonacci and Padovan series, to name a few. Incorporating, combining and ultimately exceeding much of the same number magic, the DNA double helix also exhibits a surprising and welcomed characteristic...in fact they all do: A beautiful visual pattern in numbers.
Why should that be? Who is looking? Why should there not only be patterns in numbers mathematically, but patterns in numbers visually...and very importantly...aesthetically pleasing in the simplest form to the outright magnificent beauty of the DNA double helix.
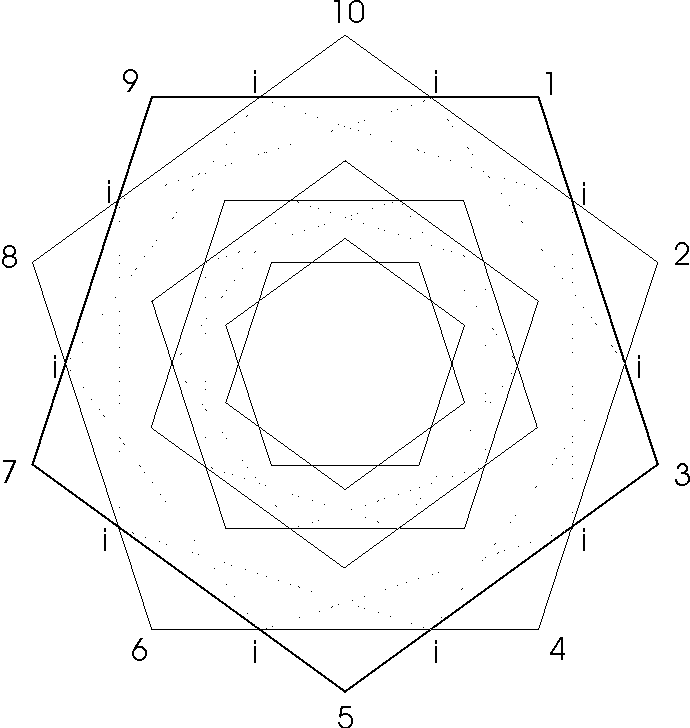
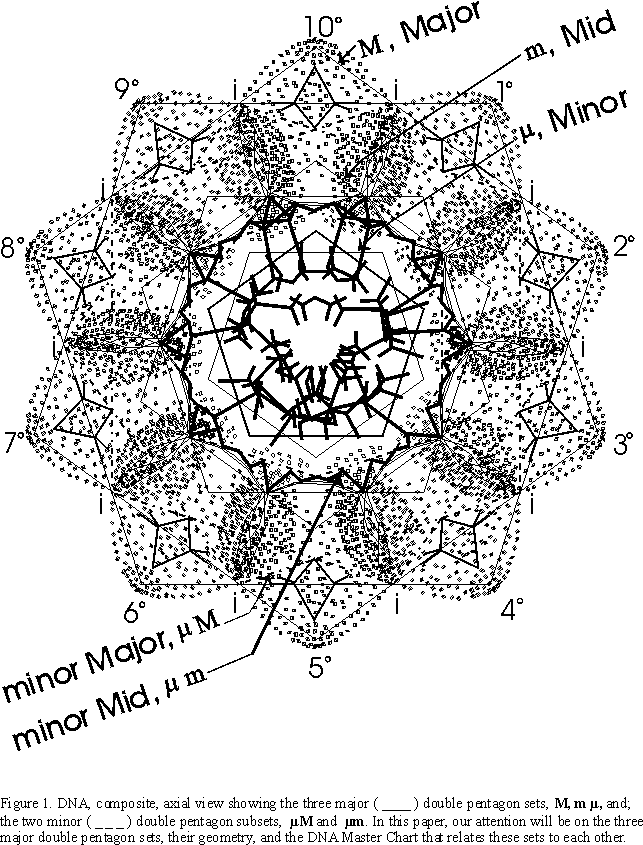
If one looks down the axis of the DNA double helix in a composite view...that is, one complete 360° rotation.. .a wonderful visual pattern of concentric double pentagon (decagons) is revealed.
Each 360° rotation of the helical coil contributes 10 sugar (deoxyribose)-phosphate groups connected in the center to the other helical coil running in the opposite direction by the complementary nucleotide bases ( the genetic code bases). Such a sugar-phosphate-nucleotide base unit is called a nucleotide. The nucleotides are symmetrically justified in the double helix so as to produce the double pentagon (Figure 1.).
Our plan is to start simple, with simple principles, and demonstrate how some of the possible diversity is inherent in the simple relationships explored. There are many, many possible avenues of approach and the one we have chosen is simple, clear and mysterious enough to start.
The simplest geometric pattern of the DNA axial view reveals three major double pentagons...major (M), mid (m), and minor (m). (Two additional double pentagons.. subsets of the M and m double pentagons which reveal even more detail…will be deferred .)
Each pentagon size becomes defined by the other two pentagon sizes by intersection (i) crossings directly or by connections of parallel (P) lines between intersections, thus (Pi), parallel intersections (Figure 2.).
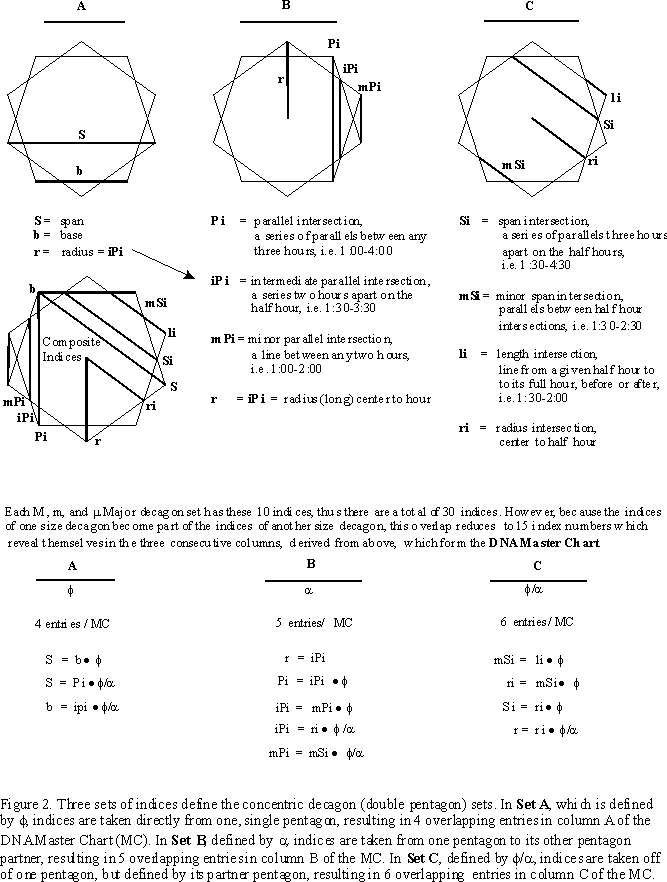
While the number patterns in a given pentagon are many, the patterns between double pentagons and concentric pentagons are truly astonishing, as we develop the basis for the DNA Master Chart (Table I.).
If we start in column A with the base (see Figure 2.) and a span of the smallest minor pentagon (m), let b=1.000, then S=1.618 which of course is f, the Golden Mean.
It follows then, that when b=1.618, S=2.618 in the mid pentagon, m, and that 2.618, S=4.236 in the major pentagon, M, as:
S = b · f , m · f = m, and m · f = M.
Each pentagon is larger by a factor of f, and thus the span of the smaller sized pentagon becomes the base of the next.
Now that we have these measurements fixed, we look at column B and find that for the m pentagon mPi=0.5264, iPi=0.85179 and Pi=1.3782. For the m pentagon we have mPI=0.85179, iPi=1.3782 and Pi=2.2300. And for the M pentagon set we have mPi=1.3782, iPi=2.2300 and Pi=3.608, giving a net of 5 different entries for the three different sized, concentric pentagon sets as:
MPi · f = iPi and iPi · f = Pi.
The indices for each pentagon set are progressively overlapped, as in column A. The Pi of m becomes the iPi of m, and the mPi of M. Notice that the radius, r, is equal to iPi for a given pentagon set.
Finally, in column C we find for the m pentagon set, li=0.2771, mSi=0.4484, ri=0.7255 and Si=1.1739. For the m set, li=0.4484, mSi=0.7255, ri=1.1739 and Si=1.899, while for the M set, li=0.7255, mSi=1.1739, ri=1.8995 and Si=3.0735, for a net of 6 entries covering the m, m and M sets. The relationship holds as:
li · f = mSi, mSi · f = ri, and ri · f = Si.
A relationship between the vertical components any given column A, B or C has been shown to be progressively increased by the factor of the Golden Mean, f, such that:
f = A/A = B/B = C/C.
A relationship between the horizontal components, that is across columns A, B and C is:
Column C · 1.1739 = column B
Column B · 1.1739 = column A
Column C · 1.1742 = column A.
3.1 THE DNA MASTER CHART (MC)
Because column A contains within itself, f = 1.618, subtitle column A, f. Since column B contains within itself, a=1.378, subtitle column B, a. Likewise, column C, containing within itself, f/a =1.1739, will be subtitled the f/a column. Thus:
A = B · C = f = 1.61803 = a · f/a
B = A/ C = a = 1.37824 = f · a.f
C =A/ B = f/a = 1.1739 = B/ C = a2/f , as
A2 = B3 = 1.6182 = 1.378243 = f 2 = a3.
C2 = B = 1.17392 = 1.37824 = a
C3 = A = 1.17393 = 1.61803 = f
f =1.6180339 is the Golden Mean, the Divine Proportion of antiquity. This ideal growth ratio is approximated by the ratios of the Fibonacci Series. The pentagon is obviously loaded with f. The Golden Mean has been used for centuries by the best artists, mathematicians, architects, designers and engineers. What is not appreciated is that the pentagon (and its relationship to its partner, resonate and concentric pentagons) is loaded with a=1.3782407, an irrational number closely related to f, a number which has intrigued theoretical physics. This strange number, which appears to come from nowhere, is a pure number, that is one without units, and describes the strength of the electromagnetic interaction at its most fundamental level. In physics it is a fundamental constant of Nature and is called the Fine Structure Constant (a=1.374). Its mystery comes in large part because there is no precedent or explanation for its value and yet here it is in the most primitive level of number proportion and pattern within the geometry of the pentagon…buried in the axial structure of that singular molecule which has allowed us to ask what of the beauty of this DNA double helix.
Now, let us see what sort of magic the MC reveals about the concentric, double pentagon patterns of the double helix. To note is that every number on the MC relates directly to a length on the double pentagon pattern proportionally. That is, the MC reveals the relationship between the numbers, not the numbers themselves. The MC is arbitrarily based on the base, b, of the m pentagon being assigned the value of 1.000, and all the other numbers follow from this proportionally. This is the simplest length to start with, revealing the three fundamental numbers, f=1.61803, a=1.3782 and f/a=1.1739, as the next three numbers progressing in the chart as it moves from right to left, bottom to top…column C to B to A, up and back to column C to B to A (Table I.).
| A | B | C |
| f | a | f / a |
| __________ | __________ | __________ |
| 199.0050 | 169.5117 | 144.3906 |
| 122.9913 | 104.7644 | 89.2387 |
| 76.0132 | 64.7480 | 55.1523 |
| 46.9787 | 40.0164 | 34.0860 |
| 29.0344 | 24.7315 | 21.0663 |
| 17.9443 | 15.2850 | 13.0197 |
| 11.0902 | 9.4466 | 8.0466 |
| 6.8541 | 5.8383 | 4.9731 |
| [4.2361] | [3.6083] | [3.0735] |
| [(2.618034)] | [(2.23004)] | [(1.89955)] |
| ({1.6180339}) | [({1.3782407})] | [({1.1739850})] |
| {1.0000000} | ({0.851799}) | [({0.72556})] |
| 0.6180338 | {0.52644} | ({0.44842}) |
| 0.38196 | 0.32536 | {0.27714} |
| 0.23607 | 0.2011 | 0.1713 |
| 0.1459 | 0.1243 | 0.1059 |
| 0.0902 | 0.0768 | 0.0654 |
| 0.0558 | 0.0475 | 0.0404 |
| 0.0344 | 0.0293 | 0.0250 |
| 0.0213 | 0.0181 | 0.0154 |
| ............................. | ............................. | ............................. |
| S, b 4 entries net for M, m, m |
Pi, iPi = r, mPi 5 entries net for M, m, m |
Si, ri, mSi, li 6 entries net for M, m, m |
Table I. DNA Master Chart. One full set of three concentric double pentagons generates 15 net indices for columns A, B and C. The indices in column A are derived from a single pentagon, in column B from pentagon to another within a double pentagon set, and in column C from a single pentagon, but defined by the crossing of its partner pentagon. Each column increases vertically by f = 1.618. Each column increases horizontally in going from column C to B, or column B to A, by f /a =1.1739.
3.2 FIVE SIMPLE RULES OF THE DNA MASTER CHART
1.) Every number is the sum of the two numbers below it in its own column. (Every number , when subtracted from the number above, generates the dividend below, and, to within 0.3%: every number added to the number up 6 steps equals the number 8 steps up, and, every number added to the number up 11 steps equals the number up 12 steps, of course.)
2.) Every number multiplied times every number equals a number on the chart. Every number on the MC represents the product of two other numbers on the chart and follows the following pattern:
| Products zeros | 12 | 10 | 8 | |
| the pattern at the | 6 | 4 | 2 | steps from 0 |
| square root of the | 0 | 2 | 4 | |
| number chosen. | 6 | 8 | 10 |
For example, 17.91/2= 4.236 = this is zero pattern mark. Pick a number from the MC, locate its pattern number from above, then go sequentially thru the chart that number of pattern steps, and now that number times the original number from the MC will equal 17.9. So picking 11.090 we see it is located at pattern position 12, therefore go down the chart 12 steps to 1.618, and the product of these two numbers equals the 17.9 we started with. Another…pick 15.28, which is 16 pattern steps, go down 16 steps to 1.173, the product of these two is 17.9.
3.) The square or square root of every number patterns as:
| Square or | 9 | 8 | 7 | |
| Square root | 6 | 5 | 4 | steps from 0 |
| zeros on | 3 | 2 | 1 | |
| MC at | 0 | 1 | 2 | |
| 1.0000 | 3 | 4 | 5 |
For example, (1.618)2 = 2.1618 = up 3 steps from 1.618.
For example, (4.236)2 = 17.94 = up 9 steps from 4.236.
To find the square root, divide the step number by 1/2.
For example, 17.94 1/2 = 18 steps/2 = 9 steps down to 4.236.
Higher exponential powers, i.e. x3, x4, x5…can also be found by combining (steps) · (operations).
For example, 1.3785 = 1.3782 · 1.3781 · 1.3781 · 1.3781 = 1.3782 is up 2 steps · 4 operation = up 8 steps from 1.378 = 4.973.
4.) The inverse of every number follows the pattern similar to the products rule (2.) above, except for zeroing:
| Inverse | 18 | 16 | 14 | |
| pattern | 12 | 10 | 8 | steps from 0 |
| zeros | 6 | 4 | 2 | |
| at 1.000 | 0 | 2 | 4 |
5.) Every number on the MC can be any one of the three sides of a right triangle as:
base, b (short side) marked side a
height, h (long side) marked side b
hypotenuse (diagonal) marked side c
such that:
c2 = a2 + b2
First pick any number on the MC from column A, B or C as the short base side, a. Then the number directly above it is the long height side, b, and the sequential number after side b, is the hypotenuse side, c.
For example:
| A | B | C | |
| 21.0663 = c | |||
| b = 17.9443 | 15.2850 | 13.0197 | |
| a = 11.0902 |
Note that the MC value for the hypotenuse is systematically off from the calculated value by about 0.148%. Calculated from the Pythagorean Theorem:
a2 + b2 = c2 = 11.0902 2 +17.94432 = 21.09482
And finally, the area, A, of any right triangle can easily be found on the MC by taking 1/2 of the MC number which is vertically up from the long side, b, by the number of sequential steps shown in the pattern:
| Area | 12 | 11 | 10 | |
| pattern | 9 | 8 | 7 | steps from 0 |
| zeros | 6 | 5 | 4 | |
| at | 3 | 2 | 1 | |
| 1.61803 | 0 | 1 | 2 |
For example, a triangle of height 6.8541, go up 9 steps from 6.854 to 29.0344 and divide by 2 to get 14.5172. To calculate the area in the conventional manner:
A = 1/2 base · height = 1/2 a · b = (4.2361)(6.8541) = 14.173
3.3 RELATING MC RIGHT TRIANGLE AREAS
For simplicity sake, if we just take the 12 hypotenuses derived from the MC in which both the base and height (sides a and b) of the triangle are inclusive to the 15 M, m and m double pentagon set indices (arbitrarily chosen here from 1.1739 to 13.0198) a Fibonacci series pattern emerges upon comparing the areas of the 12 right triangles so formed (Figure 3.). Because column C of the MC forms vertically by f · x, this pattern follows naturally from that source. And because column C times 1.1739 equals column B, and column B times 1.1739 equals column A .
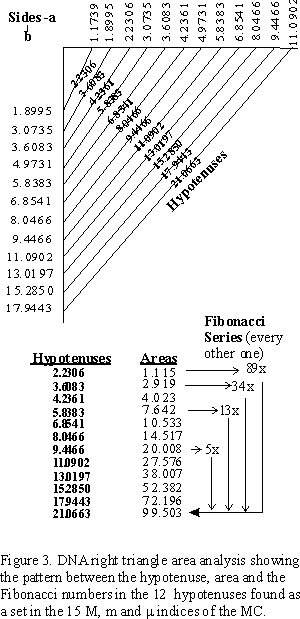
Let's assign 1.1739 = g , so that we have:
g = 1.173985
g 2 = 1.1739852 = 1.378241 = a
g 3 = 1.1739853 = 1.618034 = f
g 4 = 1.1739854 = 1.899546 = a 2 = gf
g 5 = 1.1739855 = 2.230040 = a f
g 6 = 1.1739856 = 2.618034 = a 3 = f2
g 7 = 1.1739857 = 3.073532 = a 2f
g 8 = 1.1739858 = 3.608281 = a 4 = a f2
This reveals some fundamental right triangles all derived from the DNA Master Chart (Figure 4.).
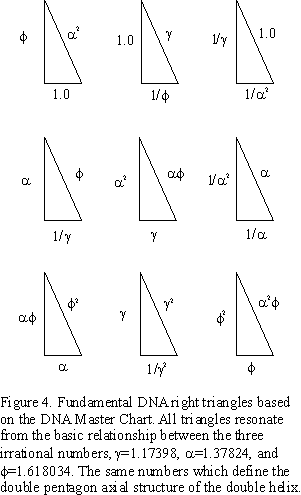
On the MC, every side a can become a side b which can become a side c, or hypotenuse. The area of all triangles can be found on the chart, once divided by two. By taking these overlapping triangle indices and joining them together, a Master DNA Triangle is formed, revealing the intimate relationship between the triangle, the pentagon, the Golden Mean (f = 1.618034), and its two generators, or drivers, a = 1.37824 and g = f /a = 1.173985. Figure 5. Table II.
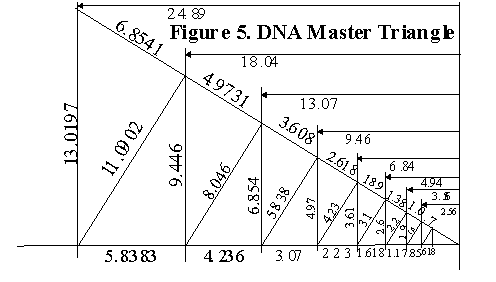
Figure 5. DNA Master Triangle from the DNA MC.
| Base side | Height side | Hypotenuse | Area | Area x 2 |
| a | b | c | A | 2A |
| __________ | __________ | __________ | __________ | __________ |
| 104.764 | 169.512 | 199.005 | ||
| 89.239 | 144.391 | 169.512 | ||
| 76.013 | 122.991 | 144.391 | ||
| 64.748 | 104.764 | 122.991 | ||
| 55.152 | 89.239 | 104.764 | ||
| 46.979 | 76.013 | 89.239 | ||
| 40.016 | 64.748 | 76.013 | ||
| 34.086 | 55.152 | 64.748 | 939.961 | |
| 29.034 | 46.979 | 55.152 | 681.999 | |
| 24.732 | 40.016 | 46.979 | 494.832 | |
| 21.066 | 34.086 | 40.016 | 359.033 | |
| 17.944 | 29.034 | 34.086 | 260.501 | |
| 15.285 | 24.732 | 29.034 | 189.010 | |
| 13.020 | 21.066 | 24.732 | 137.138 | |
| 11.090 | 17.944 | 21.066 | 99.503 x 2 | = 199.006 |
| 9.447 | 15.285 | 17.944 | 72.196 x 2 | = 144.392 |
| 8.047 | 13.020 | 15.285 | 52.382 x 2 | = 104.764 |
| 6.854 | 11.090 | 13.020 | 38.007 x 2 | = 76.014 |
| 5.838 | 9.447 | 11.090 | 27.576 x 2 | = 55.152 |
| 4.973 | 8.047 | 9.447 | 20.008 x 2 | = 40.016 |
| 4.236 | 6.854 | 8.047 | 14.517 x 2 | = 29.034 |
| 3.608 | 5.838 | 6.854 | 10.533 x 2 | = 21.066 |
| 3.074 | 4.973 | 5.838 | 7.642 x 2 | = 15.284 |
| 2.618 | 4.236 | 4.973 | 5.545 x 2 | = 11.090 |
| 2.230 | 3.608 | 4.236 | 4.023 x 2 | = 8.046 |
| 1.899 | 3.074 | 3.608 | 2.919 x 2 | = 5.838 |
| 1.61803 | 2.618 | 3.074 | 2.118 x 2 | = 4.236 |
| 1.37824 | 2.230 | 2.618 | 1.537 x 2 | = 3.074 |
| 1.17398 | 1.899 | 2.230 | 1.115 x 2 | = 2.230 |
| 1.000 | 1.61803 | 1.899 | 0.809 x 2 | = 1.618 |
| 0.852 | 1.37824 | 1.61803 | 0.587 x 2 | = 1.174 |
| 0.726 | 1.17398 | 1.37824 | 0.426 x 2 | = 0.852 |
| 0.618 | 1.000 | 1.17398 | 0.309 x 2 | = 0.618 |
| 0.526 | 0.852 | 1.000 | 0.224 x 2 | = 0.448 |
Table II. Bold print shows where the value found in the 2A column may appear as any one of the three sides of a right triangle formed in the DNA Master Chart.
[ As noted above, the main section of the Number Patterns in DNA has been given its own title, GoDNA: The Geometry of DNA , and a separate section to go to view this work. This section, has also been extracted from Patterns In Number (PIN), reworked and adapted for the web as: SCoDNA: The Structure & Chemistry of DNA (axial view). It builds on the foundation laid down in GoDNA. It is for those who wish to get deep into the design (and chemistry) of the DNA double helix as presented in the composite axial view. Others may want to skip this section altogether but I do hope you will peruse GoDNA to see first hand the marvelous number magic and pattern. For those who are digging in, you will need to access GoDNA and the Figures and Tables contained within, to proceed from here.]
The ability to recognize, incorporate and replicate oneself...especially amidst the sea of diversity, the winds of chance, the lands of opportunity...is to organize one's energies to overcome those forces of entropy. The DNA double helix molecule accomplishes such feats by means of the very same self-recognizing, self-incorporating and self-replicating attributes of the very geometry upon which it is built. The DNA Master Chart has given us a glimpse, and I am sure it is only a partial view, on how that might be done. The beauty of all life forms is a reflection of the inner beauty of that natural organizing logic and form within.
REFERENCE
This work is based on simple concepts on elementary geometry, driven by a love for pattern seen in numbers, as in Nature. The simplicity defies the diversity, yet it is through a combination of fixed, almost rigid and constant symmetry with limited, asymmetric variables that the fabric of life is woven. From the original computer generated imagery of DNA by the pioneering Robert Langridge (http://www.cgl.ucsf.edu/home/rl/index.html) over 20 years ago, I analyzed and subsequently deconstructed the image pattern into a number of geometric forms, the primary ones being a series of concentric double pentagons. In 1995 I rebuilt the pattern on the surface of a large sculpture ("Out of Africa, from mime to five, DNA").That same year I had started an ambitious paper: "The Geometry of Music, Art and Structure...linking Science, Art and Esthetics". Revised in 1996 and further revised and condensed in the final published version in 1998. My work on the Geometry of DNA was a small part of this work. I more fully developed GoDNA in the next interim work: "Pattern in Number...from Primes to DNA" in 1997, and have since readied it for formal publication in Part 2 of "The Geometry of Music, Art and Structure...linking Science, Art and Esthetics". The ideas presented in the white papers were part of my gallery shows at the former Montage Gallery in Portland, Oregon in the mid 1990's.
"The Geometry of Music, Art and Structure...linking the esthetics of Art and Science", Part 1,
was presented at the 8th ICECGDG (International Conference on Engineering Design Graphics and
Descriptive Geometry, sponsored by the International Society for Geometry and Graphics, the Japan
Society for Graphic Science, and the Engineering Design Graphics Division of the American Society
for Engineering Education; hosted by the College of Engineering, The University of Texas at Austin), 1998.
Published in the Proceedings of the 8th ICECGDG, Vol. 2, pg 378, ISGG, Tokyo, Japan, 1998
Copyright© 2001-06 Reginald Brooks, BROOKS DESIGN. All Rights Reserved.
click to go to Special Graphics Section: digital 2D works: GoDNA